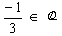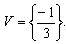Conjunto dos números inteiros relativos

Conjunto dos números inteiros relativos

Pertencem ao conjunto dos números inteiros, os números negativos e também o Conjunto dos Números Naturais. 

Os números positivos são opostos aos números negativos e os negativos opostos aos positivos. 
Sua representação é feita pela letra Z maiúscula. 

Z = {..., -4, -3, -2, -1, 0, +1, +2, +3,...} 

Observações: os números negativos são sempre acompanhados pelo sinal de negativo 
(-) (à sua frente) e os positivos são acompanhados pelo sinal positivo (+) ou sem sinal nenhum. O zero não é positivo e nem negativo. 

♦ Inteiros não – nulos 
São os números inteiros, menos o zero. 
Na sua representação devemos colocar * ao lado do Z. 
Z* = {..., -3, -2, -1, 1, 2, 3,...} 

♦Inteiros não positivos 
São os números negativos incluindo o zero. 
Na sua representação deve ser colocado - ao lado do Z. 
Z_ = {..., -3, -2, -1, 0} 

♦Inteiros não positivos e não – nulos 
São os números inteiros do conjunto do Z_ excluindo o zero. 
Na sua representação devemos colocar o _ e o * ao lado do Z. 
Z*_ = {..., -3, -2, -1} 

♦Inteiros não negativos 
São os números positivos incluindo o zero. 
Na sua representação devemos colocar o + ao lado do Z. 
Z + = { 0,1 ,2 ,3, 4,...} 
O Conjunto Z + é igual ao Conjunto dos N 

♦Inteiros não negativos e não - nulos 
São os números do conjunto Z+, excluindo o zero. 
Na sua representação devemos colocar o + e o * ao lado do Z. 
Z* + = {1, 2, 3, 4,...} 
O Conjunto Z* + é igual ao Conjunto N*

COMO RESOLVER EQUAÇÃO

Resolução de uma equação

       Resolver uma equação consiste em realizar uma espécie de operações de operações quenos conduzem a equações equivalentes cada vez mais simples e que nos permitem,finalmente, determinar os elementos do conjunto verdade ou as raízes da equação.Resumindo:

Resolver uma equação significa determinar o seu conjunto verdade, dentro do conjunto universo considerado.

    Na resolução de uma equação do 1º grau com uma incógnita, devemos aplicar os princípios de equivalência das igualdades (aditivo e multiplicativo). Exemplos:

• Sendo   , resolva a equação    .

                           MMC (4, 6) = 12

                               

                               -9x = 10       =>   Multiplicadorpor (-1)

                                9x = -10

                               

   Como  ,então .

• Sendo , resolva a equação 2 . (x - 2) - 3 . (1 - x) = 2 . (x - 4).

            Iniciamos aplicando a propriedade distributiva da multiplicação:

2x - 4 - 3 + 3x = 2x - 8 

2x + 3x -2x = - 8 + 4 + 3

3x = -1

    

     Como  , então 

    

Equações impossíveis e identidades

• Sendo  , considere a seguinte equação: 2 . (6x - 4) = 3 . (4x - 1).

            Observe, agora, a sua resolução:

2 . 6x - 2  . 4 = 3 . 4x - 3 . 1

12x - 8 = 12x - 3 

12x - 12x = - 3 + 8

0 . x = 5

    Como nenhum número multiplicado por zero é igual a 5, dizemos que a equação é  impossível e, portanto, não tem solução. Logo, V =  Ø.

    Assim, uma equação do tipo ax + b = 0 é impossível quando  e 

•  Sendo  , considere a seguinte equação: 10 - 3x - 8 = 2 - 3x.

            Observe a sua resolução:

-3x + 3x = 2 - 10 + 8

0 . x = 0 

    Como todo número multiplicado por zero é igual a zero, dizemos que a equação possui infinitas soluções. Equações desse tipo, em que qualquer valor atribuído à variável torna a equação verdadeira, são denominadas identidades.